Modelling the spatial variability and the association with candidate driving factors in the reporting of violence against women (VAW)
Variable of interest: counts of accesses to Anti-Violence Centers (AVCs) in Apulia per residence municipality of victims
Observation period: 2021 – 2024; observation units: Apulian municipalities.
Online version (recursive); more details here
2025-09-19
Scope
Importance of AVCs
Offering shelter, legal assistance and psycological support to women victims of gender-based violence
Maintaining systematic records of reported cases, as outlined in Italian Law no.119/2013
Data collected by the Statistical Section and the Welfare Department of the Apulia Region, as part of a systematic monitoring program established under Regional Law no. 29/2014
Access to AVCs in Apulia: Incidence (I)
Log-access rate, 2021-2022
Access to AVCs in Apulia: Incidence (II)
Log-access rate, 2023-2024
Explanatory variables
Distance (
TEP) from the closest municipality hosting an AVCComponents of the Municipality Frailty Index (MFI), 2021; source: ISTAT
| Variable | Unit | Description |
|---|---|---|
| TEP | Minutes | Road travel time to the closest municipality hosting an AVC |
| ELI | Ventile | Share of employees in low productivity units |
| PGR | Rate | Population growth rate 2011–2021 |
| UIS | Ventile | Density of economic production units |
| ELL | Percentage | Population aged [25–64] with low education level |
| PDI | Percentage | Structural dependency index (population aged [0–19] or >64 over [20–64]) |
| ER | Percentage | Employment rate among population aged [20–64] |
Regression model
256 municipalities, 4 years
Standard Poisson linear regression: for \(i \in [1,256]\), and \(t \in [2021, 2024]\) we have
\[ y_{it}\mid \eta_{it}, \theta \sim \mathrm{Poisson} \left( \mathrm{E}_{it} \, e^{\eta_{it}} \right) \]
- Where
\(y_{it}\): AVC accesses in municipality \(i\) and year \(t\);
\(\mathrm{E}_{it}\): female population aged \(>14\) years (offset)
\(\eta_{it}\): linear predictor; \(\theta\): model hyperparameters
The linear predictor
- Inclusion of a multivariate latent spatial effect in \(\eta\) to account for territorial variability and overdispersion
\[\eta_{it} := X_{it}^\top \beta + Z_{it}\] - \(X\): Covariates; \(\beta\): covariate effects
\(Z_{it}\): multivariate latent spatial effect of size \(n \times k\), where \(n=256\) and \(k=4 \quad \longrightarrow\) modelled via the flexible M-Models (Botella-Rocamora, Martinez-Beneito, and Banerjee 2015)
Competing models: ICAR, PCAR, LCAR and BYM
Models (I): Intrinsic CAR
- Simplest formulation among spatial autoregressive models
\[ Z \mid \Sigma \sim \mathcal{N}_{kn} \left( 0, \Sigma \otimes (D - W)^{+} \right) \]
\(\Sigma\): \(4 \times 4\) between-fields variance-covariance matrix
\(D\): Graph degree matrix;
\(W\): Graph neighbourhood matrix
\(+\) Easy to fit and interpret
\(-\) implicitly assumes spatial autocorrelation equal to 1 \(\rightarrow\) sometimes too smooth to adequately fit data
M-models (I)
Based on the decomposition of the variance-covariance matrix as \(\Sigma := M^\top M\)
\(M\): full rank matrix, of size \(k \times k\) herein
consider \(Z\) as a combination of \(k\) independent fields \(Z_j^{(0)}\) for \(1 \leq j \leq k\), i.e. \(Z := \left(Z_1^{(0)}, \dots, Z_k^{(0)}\right) M\)
\(Z^{(0)} \sim \mathcal{N}_n \left( 0, \Omega_j \right)\) for a \(n \times n\) s.p.d. matrix \(\Omega_j\) depending:
- On the graph structure
- On an array of model-specific parameters
M-models (II)
Joint prior of \(Z\):
\[ Z \sim \mathcal{N}_{nk} \left(0, (M^\top\otimes I_n)\, \Omega \, (M \otimes I_n) \right) \] Where \(\Omega\) is block-diagonal: \[ \Omega = \begin{pmatrix} \Omega_1 & 0 & \dots & 0 \\ 0 & \Omega_2 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & \Omega_k \end{pmatrix} \]
- Three standard models for \(\Omega\) compared in next slides
Models (II): Proper CAR (PCAR)
Generalises the ICAR allowing for a proper prior density with nonsingular precision (Gelfand and Vounatsou 2003)
Introduces a spatial correlation parameter \(A := \mathrm{diag}(\alpha_1, ... \alpha_k)\), \(\alpha_j \in [0,1] \, \forall j\)
\[ \Omega = (I_k \otimes D - A \otimes W)^{-1} \]
- Limit cases:
- \(\alpha_t = 0\): independent model (\(\neq\) IID)
- \(\alpha_t = 1\): ICAR
Models (III): Leroux proper CAR (LCAR)
Also generalises the ICAR allowing for a proper density
Introduces a precision mixing parameter \(\Lambda := \mathrm{diag}(\lambda_1, ... \lambda_k)\), yet with \(\lambda_j \in [0,1] \, \forall j\) (Leroux, Lei, and Breslow 2000)
\[ \Omega_j = \left(\Lambda \otimes L + (I_k - \Lambda) \otimes I_n \right)^{-1} \] - \(L\) = graph Laplacian matrix, i.e. \(L = D-W\)
- Limit cases:
- \(\lambda_t = 0\): IID model
- \(\lambda_t = 1\): ICAR
- \(\lambda_t = 0\): IID model
Models (IV): Besag-York-Mollié (BYM)
- Actually a reparametrisation of the original BYM (Besag, York, and Mollié 1991), proposed by (Riebler et al. 2016)
\[ Z = U \Phi^\frac{1}{2} M + V (I_k-\Phi^\frac{1}{2}) M \]
\(U \sim \mathcal{N}_{kn} \left(0, I_k \otimes L_S^{+} \right)\): independent ICAR (limit case for \(\Phi = I_k\)) \(\rightarrow\) spatial dependence, where \(L_S\): scaled Laplacian (Riebler et al. 2016)
\(V \sim \mathcal{N}_{kn} (0, I_{kn})\): IID field (limit case for \(\Phi = 0\)) \(\rightarrow\) noise
\(\Phi := \mathrm{diag}(\phi_1, \dots, \phi_k)\): variance mixing parameter, \(\phi_j \in [0, 1]\, \forall j\)
Multivariate PC-prior
The parameters \(A\), \(\Lambda\) and \(\Phi\) are usually assigned a Uniform prior
A more principle-based approach is using PC-priors
- This was already done by Rieber et al. (2016) for the univariate BYM
Question: can we apply this approach in the multivariate setting, and also for PCAR and LCAR models?
Caveat: deriving analytically a PC-prior for multivariate parameters is hardly possible (Simpson et al. 2017), (Battagliese 2020) \(\longrightarrow\) workaround: Sequential derivation
PC priors: principles
Penalise the departure of a model depending on a parameter \(\theta\) from a simpler (base) one (Simpson et al. 2017):
Simple model: here, an independent, unstructured one, with \(\theta = 0\)
Departure: a measure of how the more flexible model, say \(\mathcal{M}_F\) diverges from the simple one, say \(\mathcal{M}_B \rightarrow\) distance function: \(d (\mathcal{M}_F||\mathcal{M}_B) := \sqrt{2 \mathrm{KLD}(\mathcal{M}_F||\mathcal{M}_B)}\)
Penalise: shrink the p.d.f. of \(d(\mathcal{M}_F||\mathcal{M}_B)\) at a constant rate \(\rightarrow\) exponential prior on \(d\)
Fix two parameters \(\theta_0, \mathcal{a}:\mathrm{Prob} \lbrace \theta \leq \theta_0 \rbrace = \mathcal{a}\)
A Sequential approach for the PC-prior
Let \(\theta_j\) denote either \(\alpha_j\), \(\lambda_j\), or \(\phi_j\) for \(j = 1, \dots, k\)
At each step \(j\), we test the flexible model with \(\theta_j > 0\), against the base model with \(\theta_j = 0\), all other parameters being unchanged
Then, the joint prior simply comes from the chain rule:
\[\pi(\theta) = \pi (\theta_1) \pi(\theta_2 \mid \theta_1) \dots \pi(\theta_k \mid \theta_1, \dots, \theta_{k-1})\]
- Provided that
\[ \begin{align*} \pi(\theta_j \mid \theta_1, \dots, \theta_{j-1}) = \\ =\pi(\theta_j \mid \theta_1, \dots, \theta_{j-1}, \theta_{j+1}=\dots=\theta_k=0) \end{align*} \]
PC priors: ractical findings
PC-priors available in closed formula
\(\pi(\theta)\) independent on \(\Sigma\)
\(\pi(\theta_j \mid \theta_1, \dots, \theta_{j-1}) = \pi(\theta_j)\), i.e., at each step \(j\), the prior of \(\theta_j\) is independent on other parameters
\[ \therefore \pi(\theta) = \prod_{j=1}^k \pi(\theta_j) \]
- Only needed Laplacian eigenvalues (LCAR, BYM) or eigenvalues of \(D^{-1}W\) (PCAR), both deterministic \(\rightarrow\) computed once
Univariate PCAR PC-prior
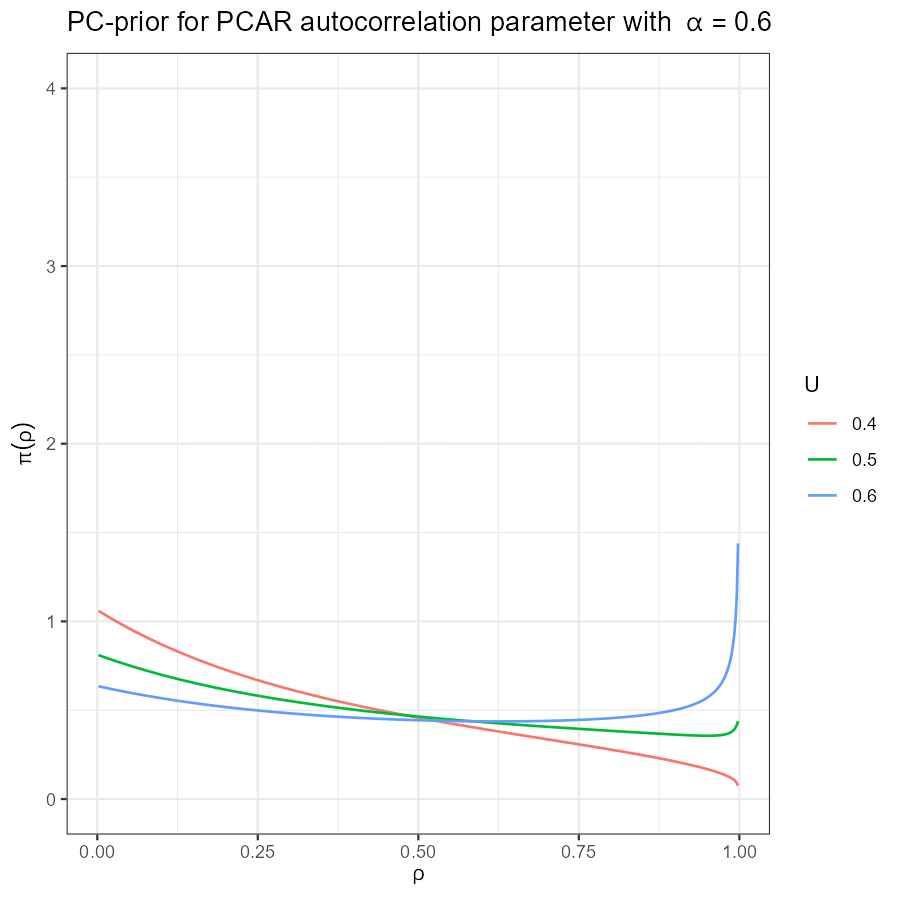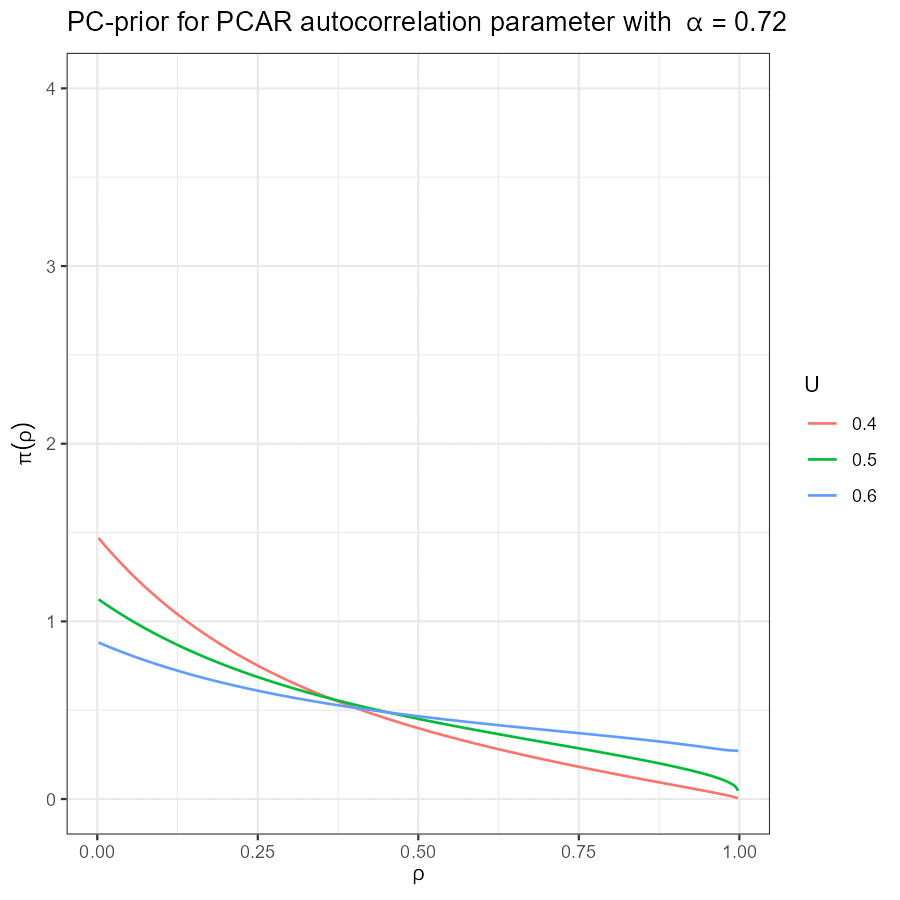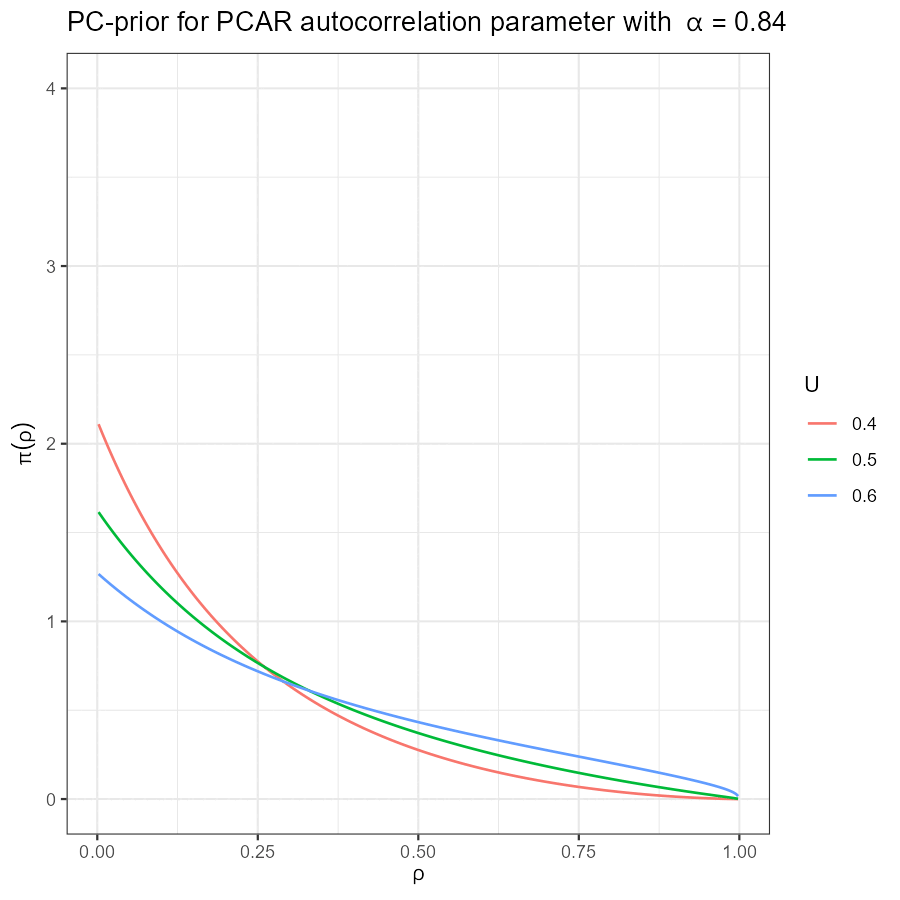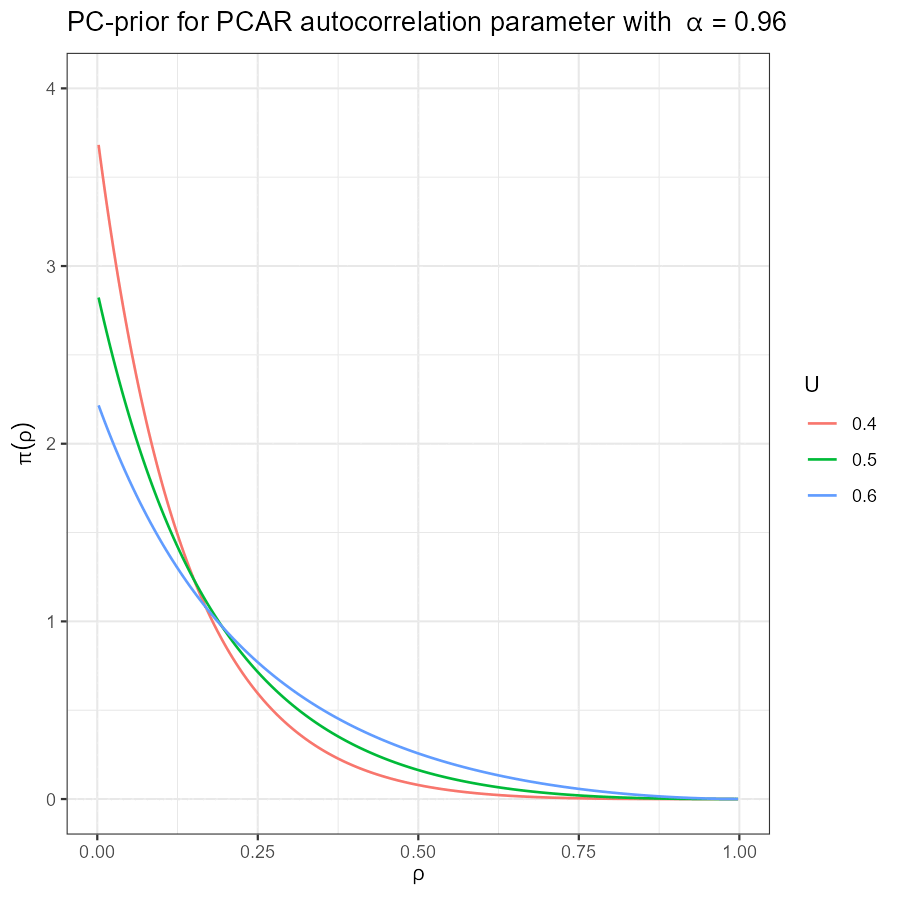
|
|
Univariate LCAR PC-prior
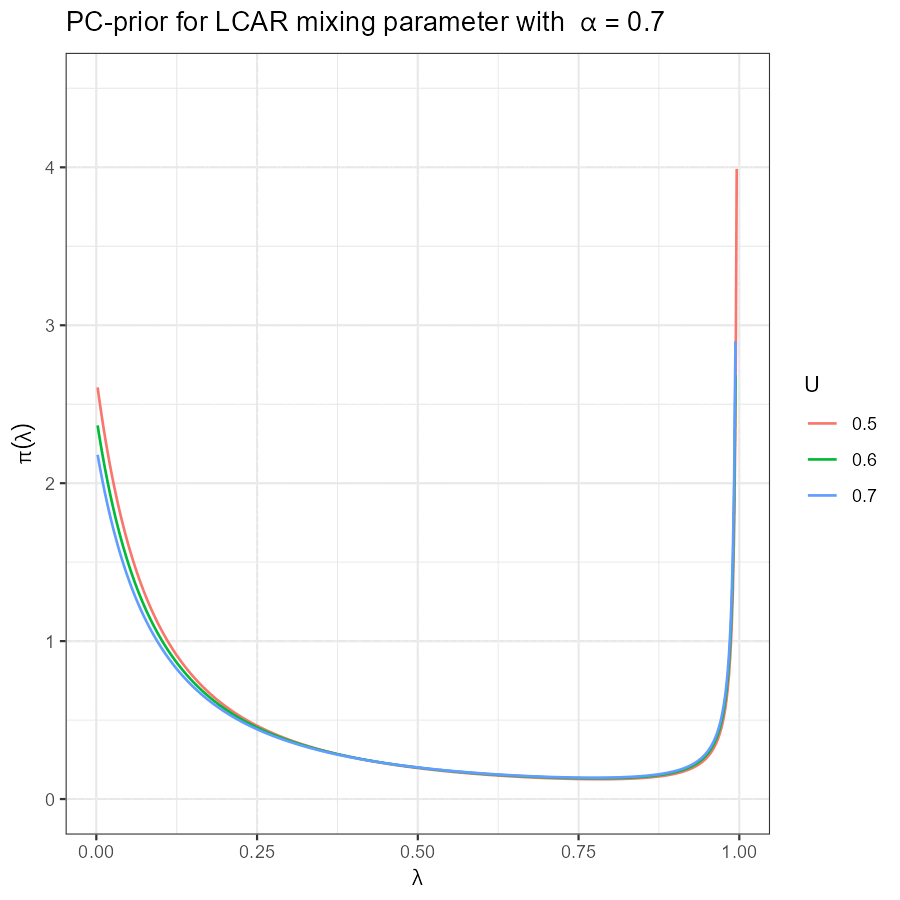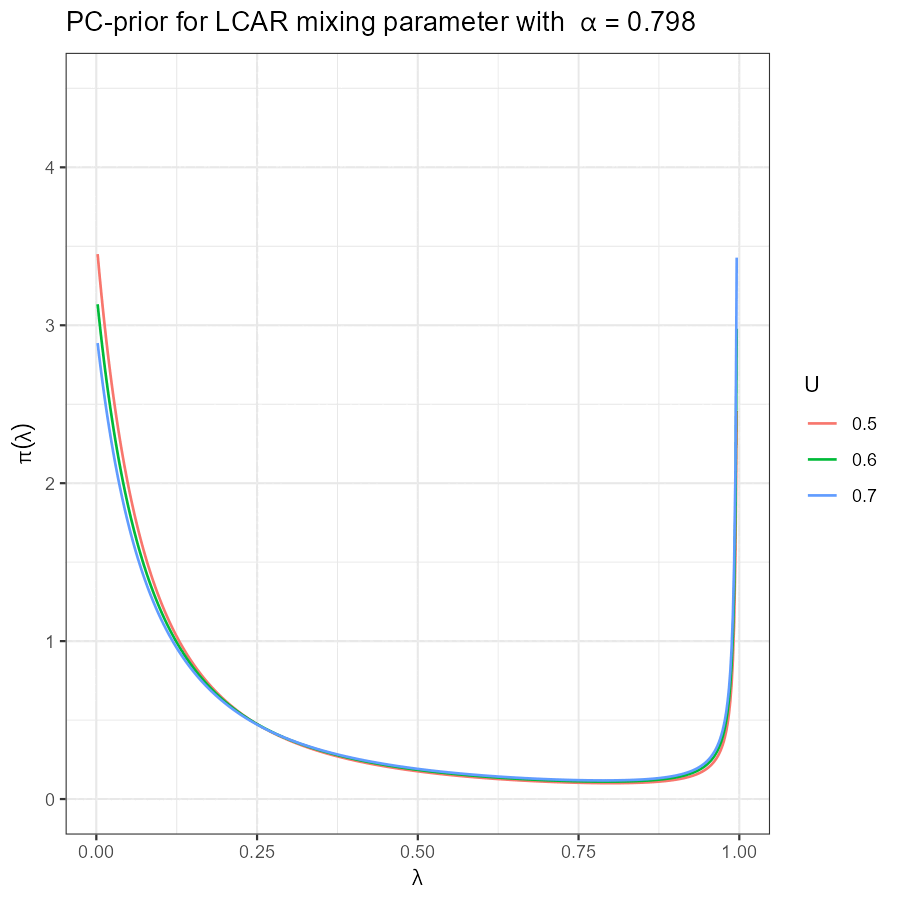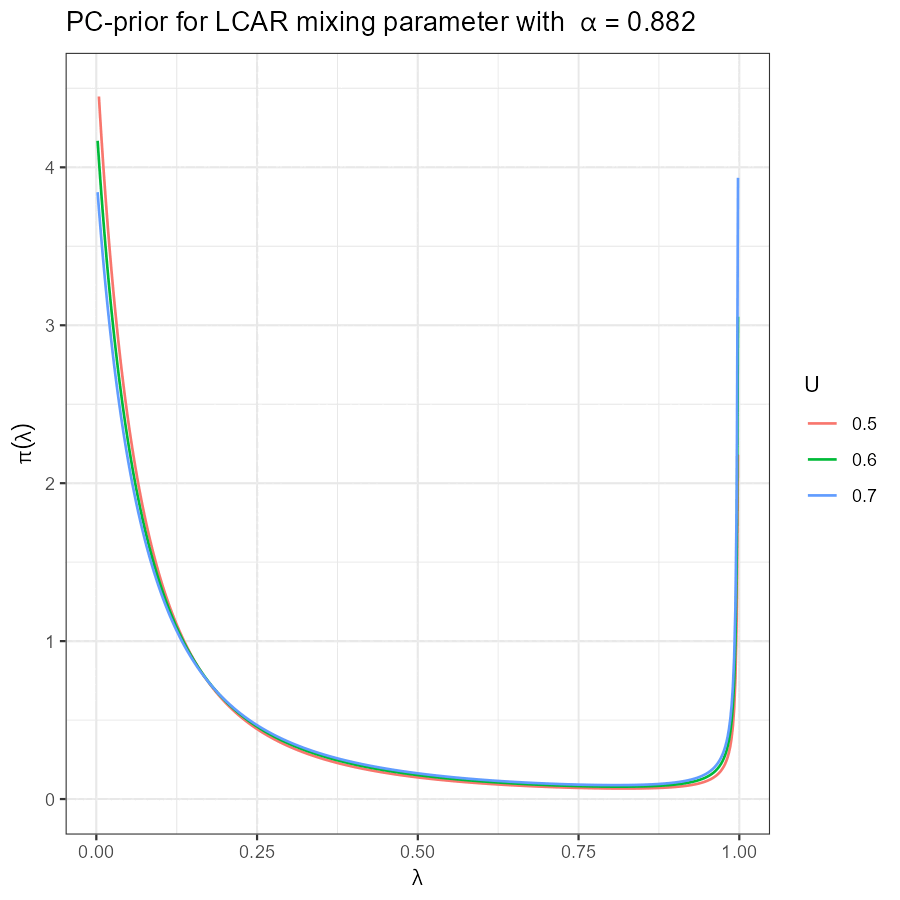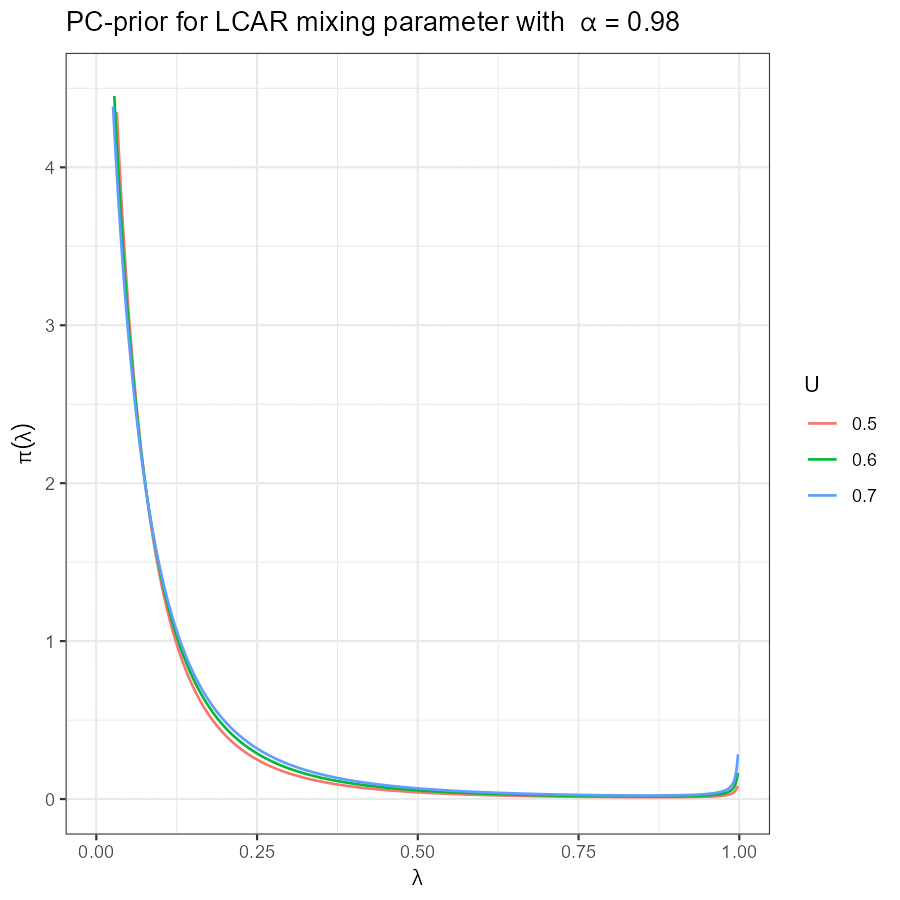
|
|
Univariate BYM PC-prior
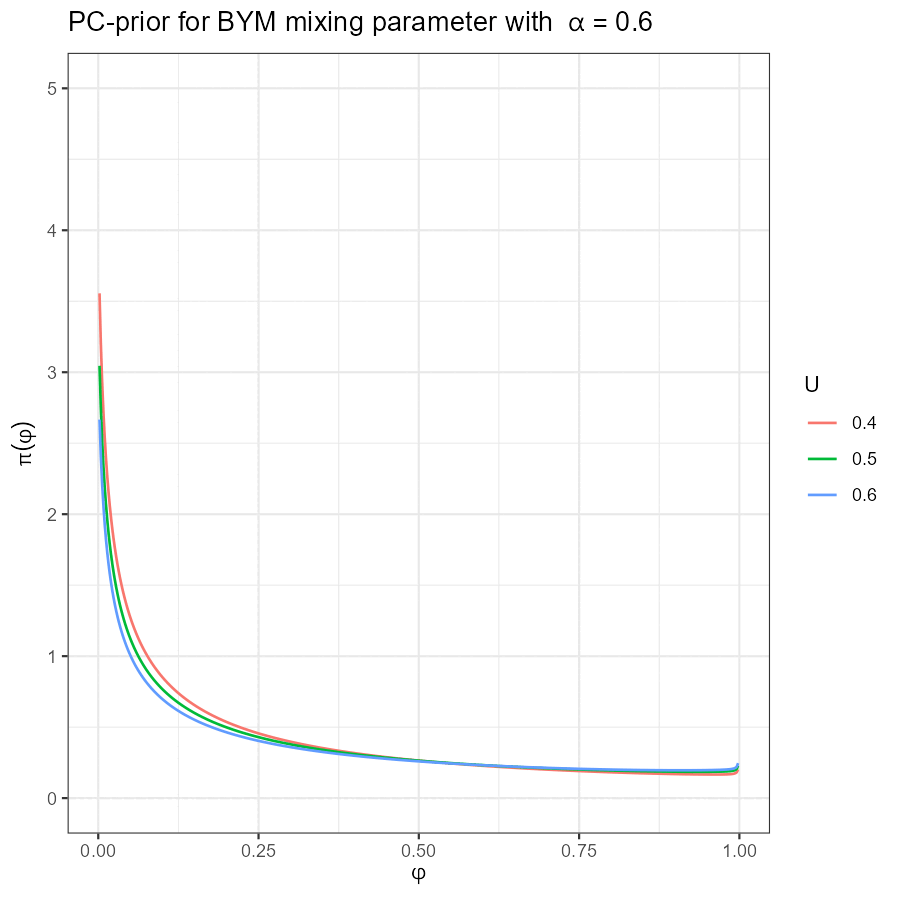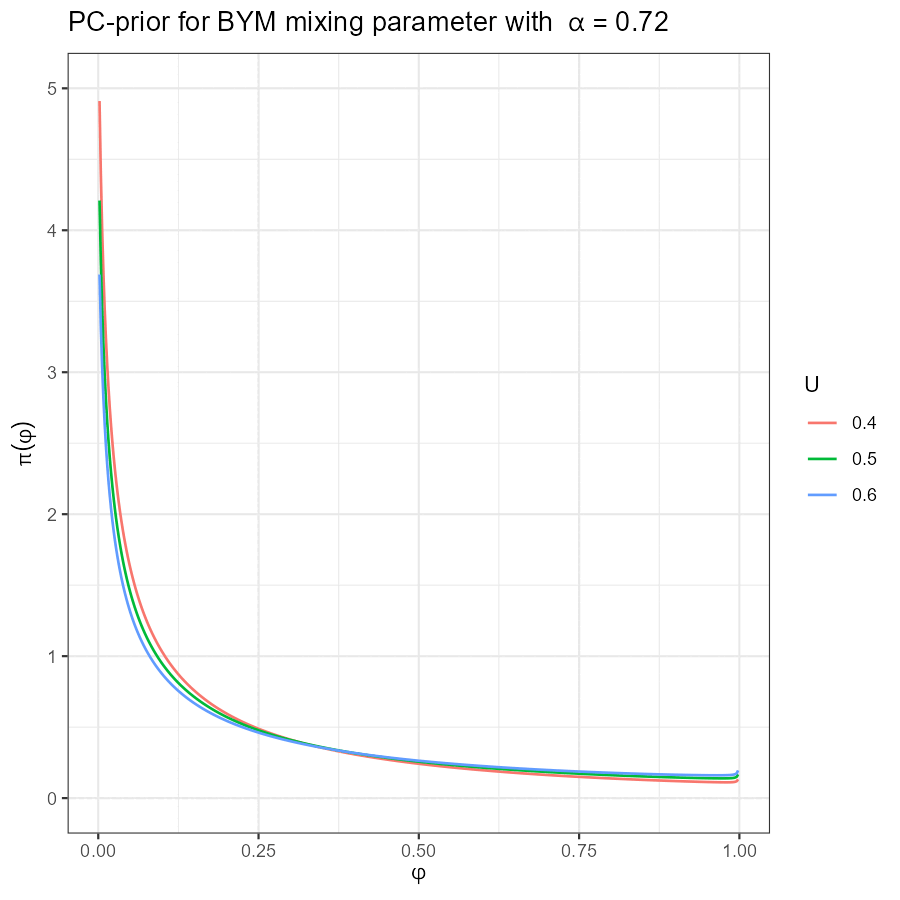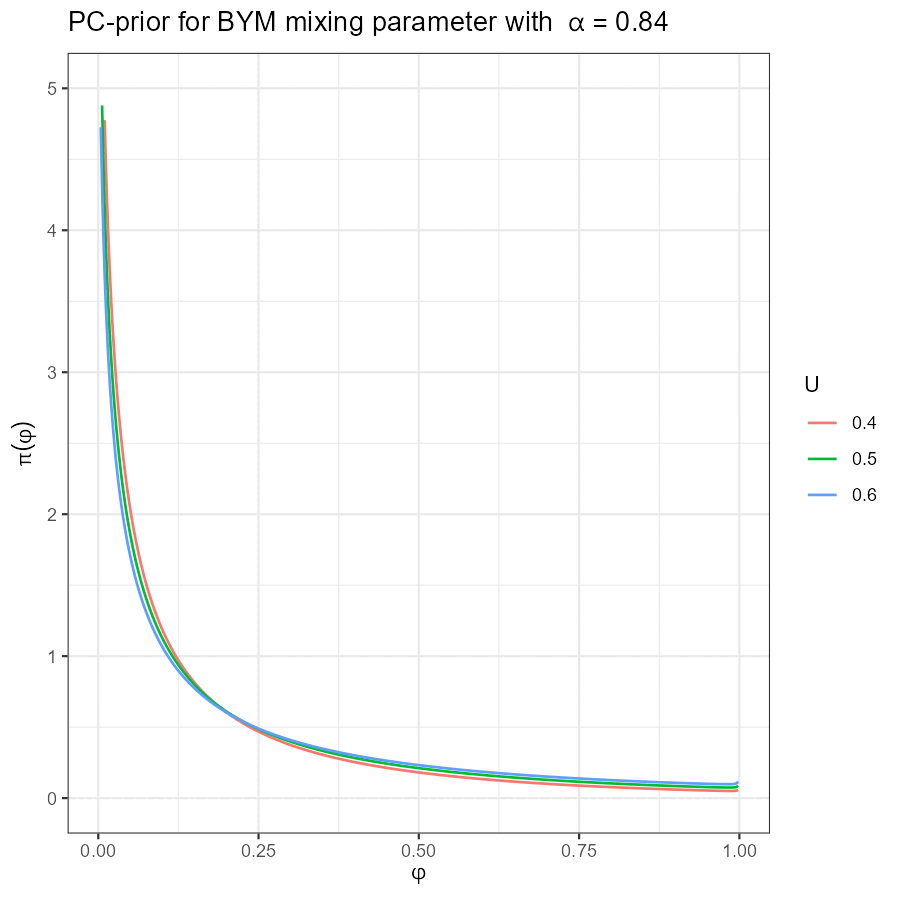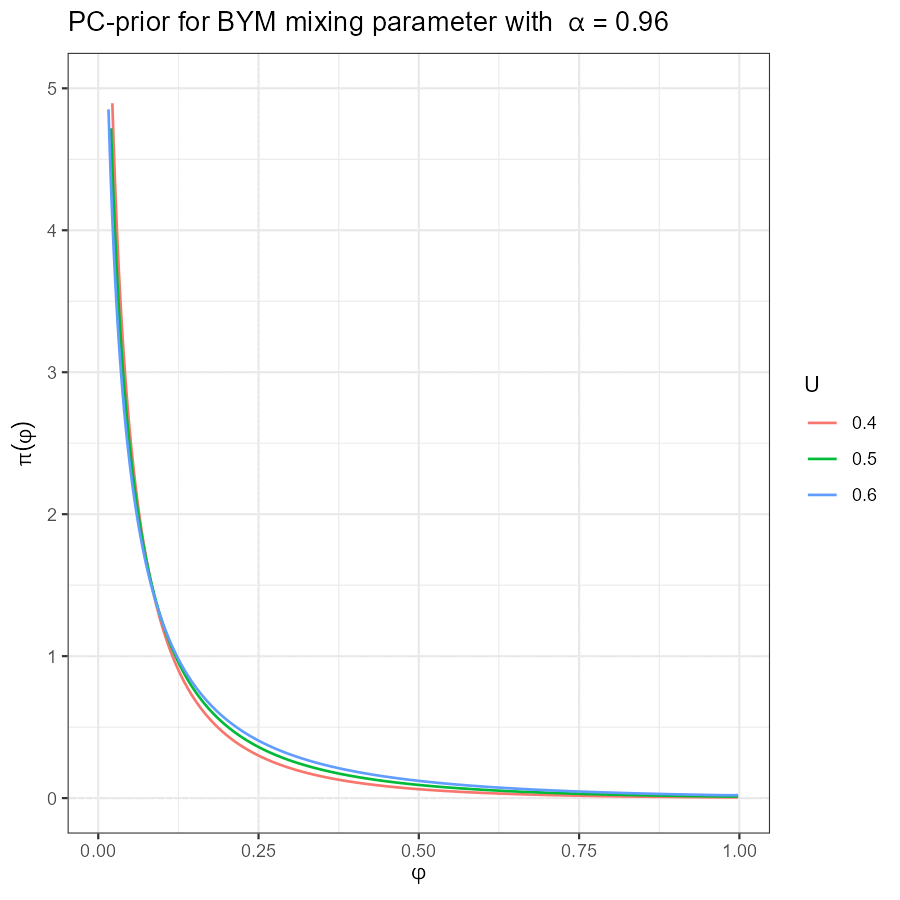
|
|
Model diagnostics
Models compared by the WAIC – Watanabe–Akaike Information Criterion (Gelman, Hwang, and Vehtari 2014). Free parameters are reported as well.
Model prior choice - BYM
Covariate effects: independent weekly informative Gaussians \(\mathcal{N}(0, 10^3)\)
\(\Sigma\): Wishart prior, with identity scale parameter and 8 degrees of freedom
\(\Phi\): PC-prior, with \(\mathrm{Prob} \lbrace \phi_j \leq 0.6 \rbrace = 0.9\) for all \(j\)
Model estimation is carried out entirely within R-INLA (Rue, Martino, and Chopin 2009) using the Variational Bayes (Van Niekerk et al. 2023) correction to the posterior mean of latent variables
Covariate effect posterior
Covariate Effects Interpretation
\(y =\) VAW occurrence \(\times\) incidents reporting rate
Twofold interpretation of covariate effects on AVC accesses
TEP: either relative ease in reporting violence in proximity of AVCs, or appropriateness of AVC placement
ELL: lower reliance on AVCs in poor education contexts
ER: lower violence occurrence in more developed areas
Hyperparameter posterior (I)
Posterior distribution of the mixing parameter (\(\Phi\))
Percentage of variation explained by spatial dependence
Hyperparameter posterior (II)
- Posterior of the variance-covariance matrix (\(\Sigma\))
Expected latent effect - BYM
Posterior values of \(\mathbb{E}[Z \mid y]\)
Possible development directions
Intepretation and modelling:
Separate factors driving the two processes of violence occurring and help seeking
\(\longrightarrow\) allocate covariates between two separate predictors: i.e. Poisson–Logistic regression (Stoner, Economou, and Silva 2019), (Polettini, Arima, and Martino 2024)
Statistical methodology:
More insight on PC prior behaviour in PCAR and LCAR models \(\longrightarrow\) simulation analysis
Extend the PC-prior approach to the correlation matrix (Freni-Sterrantino et al. 2025)
Cited works
Battagliese, Diego. 2020. “Extensions of the Univariate PC Prior.” Annali Del Dipartimento Di Metodi e Modelli Per l’Economia, Il Territorio e La Finanza (MEMOTEF), 33–46. https://doi.org/https://doi.org/10.13133/2611-6634/509.
Besag, Julian, Jeremy York, and Annie Mollié. 1991. “Bayesian Image Restoration, with Two Applications in Spatial Statistics.” Annals of the Institute of Statistical Mathematics 43 (1): 1–20.
Botella-Rocamora, Paloma, Miguel A Martinez-Beneito, and Sudipto Banerjee. 2015. “A Unifying Modeling Framework for Highly Multivariate Disease Mapping.” Statistics in Medicine 34 (9): 1548–59.
Freni-Sterrantino, Anna, Denis Rustand, Janet van Niekerk, Elias Teixeira Krainski, and Håvard Rue. 2025. “A Graphical Framework for Interpretable Correlation Matrix Models for Multivariate Regression: A. Freni-Sterrantino Et Al.” Statistical Methods & Applications, 1–39.
Gelfand, A. E., and P. Vounatsou. 2003. “Proper Multivariate Conditional Autoregressive Models for Spatial Data Analysis.” Biostatistics 4 (1): 11–15. https://doi.org/https://doi.org/10.1093/biostatistics/4.1.11.
Gelman, Andrew, Jessica Hwang, and Aki Vehtari. 2014. “Understanding Predictive Information Criteria for Bayesian Models.” Statistics and Computing 24 (6): 997–1016. https://doi.org/10.1007/S11222-013-9416-2.
Leroux, Brian G., Xingye Lei, and Norman Breslow. 2000. “Estimation of Disease Rates in Small Areas: A New Mixed Model for Spatial Dependence.” In Statistical Models in Epidemiology, the Environment, and Clinical Trials, edited by M. Elizabeth Halloran and Donald Berry, 179–91. New York, NY: Springer New York. https://doi.org/https://doi.org/10.1007/978-1-4612-1284-3_4.
Polettini, Silvia, Serena Arima, and Sara Martino. 2024. “An Investigation of Models for Under-Reporting in the Analysis of Violence Against Women in Italy.” Social Indicators Research 175 (3): 1007–26.
Riebler, Andrea, Sigrunn H Sørbye, Daniel Simpson, and Håvard Rue. 2016. “An Intuitive Bayesian Spatial Model for Disease Mapping That Accounts for Scaling.” Statistical Methods in Medical Research 25 (4): 1145–65.
Rue, Haavard, Sara Martino, and Nicholas Chopin. 2009. “Approximate Bayesian Inference for Latent Gaussian Models by Using Integrated Nested Laplace Approximations.” Journal of the Royal Statistical Society Series B: (Methodological) 71 (2): 319–92. https://doi.org/10.1111/j.1467-9868.2008.00700.x.
Simpson, Daniel, Haavard Rue, Andrea Riebler, Thiago G. Martins, and Sigrunn H. Sørbye. 2017. “Penalising Model Component Complexity: A Principled, Practical Approach to Constructing Priors.” Statistical Science 32 (1): 1–28. https://doi.org/10.1214/16-STS576.
Stoner, Oliver, Theo Economou, and Gabriela Drummond Marques da Silva. 2019. “A Hierarchical Framework for Correcting Under-Reporting in Count Data.” Journal of the American Statistical Association.
Van Niekerk, Janet, Elias Krainski, Denis Rustand, and Haavard Rue. 2023. “A New Avenue for Bayesian Inference with INLA.” Computational Statistics and Data Analysis 181. https://doi.org/10.1016/j.csda.2023.107692.